
- 配管の圧力損失はどうやって求めるの?
- 曲げ管、入口部などの計算方法も知りたい。
- EXCELで圧力損失を計算してみたい。
こんな人に向けた記事です。
こんにちは。
プラントエンジニアの火プライオンです。
この記事では、配管圧力損失の計算方法について解説します。
記事の最後には配管圧損計算の計算シート(EXCEL)を添付したので、勉強に役立ててください。
圧力損失はダルシー・ワイスバッハの式で求める
配管の圧力損失は次に示す、ダルシー・ワイスバッハの式で求めることが出来ます。
$$\Delta p=\lambda\frac{\rho u^2}{2}\frac{L}{D} $$
Δp : 圧力損失[Pa] λ:管摩擦係数 u:流体の速度[m/s]
ρ : 流体の密度[kg/m3] L : 配管長さ[m] D:配管の内径[m]
では、計算に使用する各数値を詳しく見ていきましょう。
管摩擦係数はコールブックの式で求める
乱流における管摩擦係数λは下記のコールブックの式で求めることが出来ます。
$$\frac{1}{\sqrt{\lambda}} = -2\log\left(\frac{e}{3.71D}+\frac{2.51}{Re\sqrt{\lambda}}\right)$$
λ:管摩擦係数 e:管の粗度[mm] D : 配管の内径[mm] Re:レイノルズ数
管摩擦係数はコールブックの式の左辺と右辺を満たす値となります。
手計算で求めるのは大変ですが、EXCELのゴールシーク機能を使用すれば簡単に求めることが出来ます。
グラフを読み取るのが面倒なので、僕はコールブックの式を利用するよ。
層流の場合の管摩擦係数は以下の式で簡単に求められますが、実務で使用することはあまりないと思います。
$$\lambda=\frac{64}{Re}$$
では、管の粗度とレイノルズ数の求め方について見ていきましょう。
管の粗度
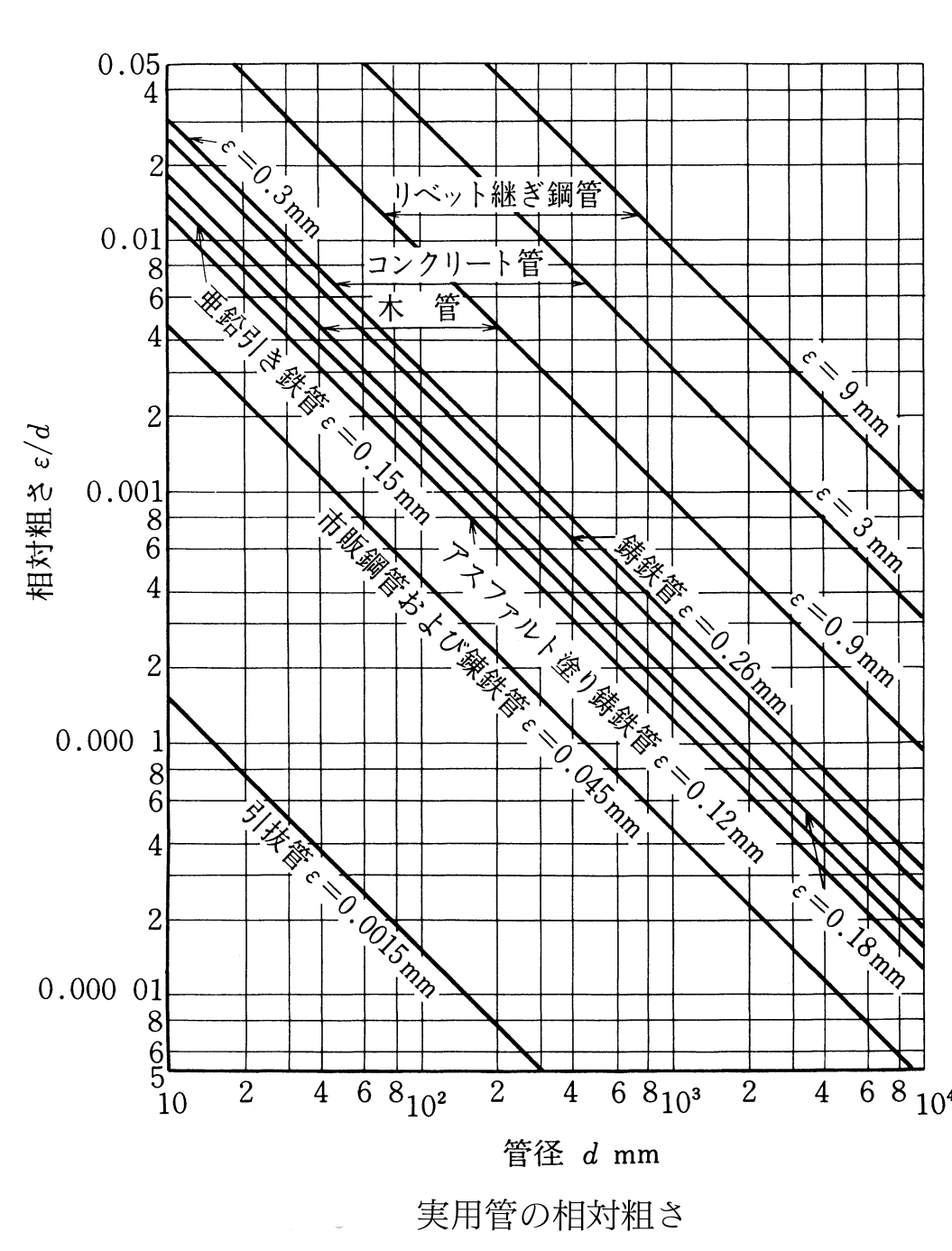
粗度は下左の表から選択して決めます。
機械工学便覧では、下右図のように表で提示されています。(縦軸がe/Dとなっているのは、ムーディ線図から管摩擦係数を求める場合に使用するからです。)
| 配管の種類 | 粗度e [mm] |
| 引抜鋼管 | 0.0015 |
| 工業用鋼管 | 0.045 |
| アスファルト塗鋳鉄管 | 0.12 |
| 鋳鉄管 | 0.26 |
レイノルズ数
レイノルズ数は下記の式で表すことが出来ます。
$$Re=\frac{Du\rho}{\mu}$$
記号の説明
D:配管の内径[m] u : 流体速度[m/s] ρ : 流体密度[kg/m3] μ : 流体の粘度[Pa・s]
流体速度
管の流速は流量を管内径で割る次式で求めます。
$$u = \frac{Q}{\frac{\pi}{4}D^2}・\frac{1}{60}$$
Q : 流量[m3/min] D : 管内径[m]
流体の密度、粘度
蒸気表や化学便覧で調べましょう。
以上で、直管の場合は、長さLを決めてしまえば、圧力損失は求めることが出来ます。
しかし、実際の配管は曲げ管や弁、配管の拡大部があります。
次は、これらの圧力損失の計算方法を見ていきます。
曲げ管や弁の圧力損失は相当長さで求める
曲げ管や弁などは、相当長さに換算して圧力損失を求めます。
相当長さとは、曲げ管や弁の圧力損失を直管の長さで表した値です。
この相当長さと直管を足し合わしてダルシー・ワイスバッハの式で圧力損失を求めます。
つまり、ダルシー・バッハの式のLは、曲げ管や弁などの相当長さをLe、直管長さをL’とすると
$$L=L’+Le$$
となります。
そして、相当長さLeは
$$Le = nD$$
で求められます。Dは配管の内径です。
曲げ管
曲げ管のnは以下のようになります。
| 項目 | n |
| 45°エルボ | 15 |
| 90°エルボ | 32 |
| Tピース | 80 |
弁類
弁のnは以下のようになります。
| 項目 | n |
| 仕切弁(全開) | 7 |
| 仕切弁(3/4開) | 40 |
| 仕切弁(2/4開) | 200 |
| 仕切弁(1/4開) | 800 |
| 玉形弁 | 300 |
| 逆止弁 | 55 |
| アングル弁 | 170 |
拡大・縮小部、出入口部の圧力損失
拡大・縮小部、出入口部の圧力損失は、別途計算します。
順番に見ていきましょう。
円すい状の拡大部の圧力損失
円すい状拡大部の圧力損失は
$$\Delta p=f・\rho\frac{(u-U)^2}{2}$$
で表せます。

そして、損失係数fは、(D/d)2=1~2の場合は下グラフを用いて広がり角度θより求まります。
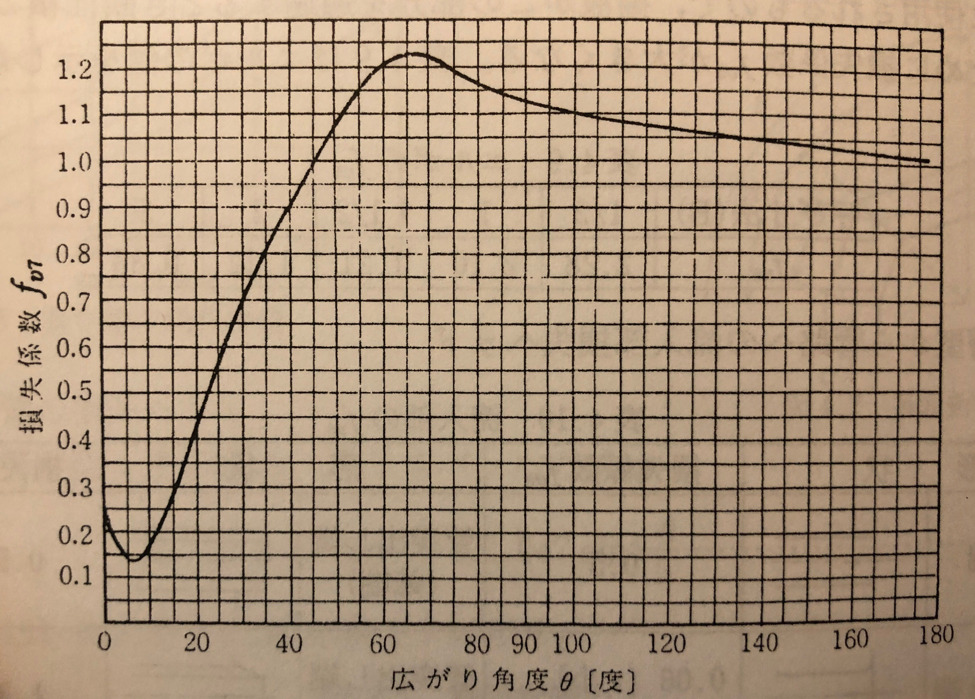
急拡大管の場合はΘ=180°とすれば良いよ!
円すい状の縮小部の圧力損失
円すい状縮小部の圧力損失は
$$\Delta p=f・\frac{\rho u^2}{2}$$
で表せます。
損失係数fは
$$f=\frac{0.025}{8sin\frac{\theta}{2}}・\left\{1-(\frac{d}{D})^4\right\}$$
となります。
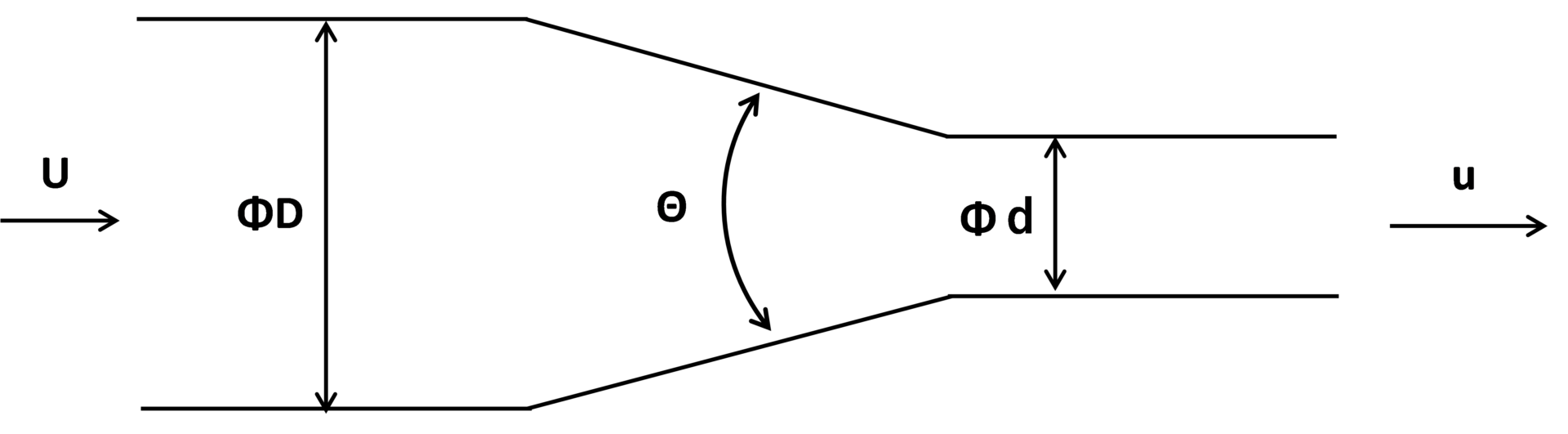
出入口部の圧力損失
出入口部の圧力損失も
$$\Delta p=f・\frac{\rho v^2}{2}$$
で表すことが出来ます。
入口部の損失係数
入口部の損失係数fは次のようになります。

出口部の損失係数
出口部の損失係数fは下図のどれでもf =1.0となります。
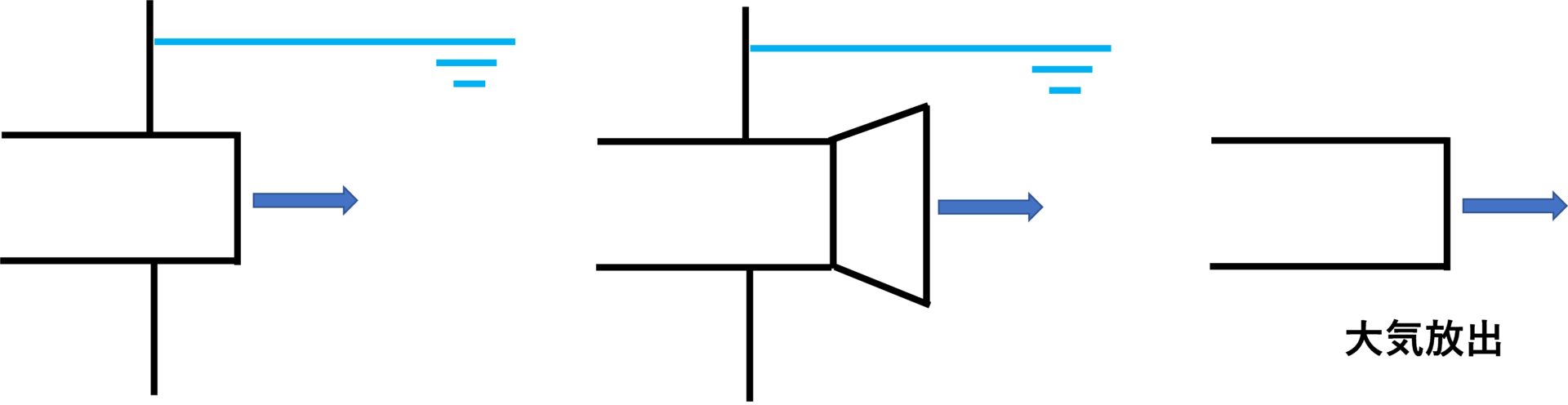
以上で、すべての圧力損失が求まりました。
まとめ
以上をまとめます。
- 配管の圧力損失はダルシー・ワイスバッハの式で求まる
$$\Delta p=\lambda\frac{\rho u^2}{2}\frac{L}{D} $$ - 圧力損失係数はコールブックの式で求まる。
$$\frac{1}{\sqrt{\lambda}} = -2\log(\frac{e}{3.71d}+\frac{2.51}{Re\sqrt{\lambda}})$$ - 曲げ管、弁類は直管相当長さに変換する。
- 拡大・縮小部、出入口部の圧力損失は別途求める。
$$\Delta=f・\frac{\rho v^2}{2}$$
計算過程をフローにしました。

配管の圧力損失計算シート【EXCEL】
以下からダウンロードしてください。
注意1)計算チェックはしておりますが、万が一間違いが有るかもしれませんので、使用の際は自己責任でお願い致します。
注意2)拡大、縮小管は考慮していません。


